

Systematic sampling is a statistical method used to select a sample from a larger population systematically and randomly. It is a widespread technique for researchers and analysts who want to gather data from a large population without surveying every individual. This method is beneficial when the population is large, diverse, or hard to reach.
This article will delve into the details of systematic sampling, including its definition and advantages. We will also provide examples of how it can be used in various research and data analysis contexts and tips on implementing it effectively. Whether you are a researcher, analyst, or simply interested in understanding this sampling method, this article will give you an understanding of what it is and how to use it for better decision-making.
Systematic sampling is a statistical method that researchers use to zero down on the desired population they want to research. Researchers calculate the sampling interval by dividing the entire population size by the desired sample size determination. It is an extended implementation of probability sampling in which each group member is selected regularly to form a sample.
Systematic sampling is a probability sampling method where the researcher chooses elements from a target population by selecting a random starting point and selecting sample members after a fixed ‘sampling interval.’
For example, in school, while selecting the captain of a sports team, most of our coaches asked us to call out numbers such as 1-5 (1-n) and the students with a random number decided by the coach. For instance, three would be called out as team captains. It is a non-stressful selection process for both the coach and the players. There’s an equal opportunity for every member of a population to be selected using this sampling bias technique.
LEARN ABOUT: Survey Sampling
Here are the steps to form a systematic sample:
Step one: Develop a defined structural audience to start working on the sampling aspect.
Step two: As a researcher, figure out the ideal size of the sample, i.e., how many people from the entire population to choose to be a part of the sample.
Step three: Once you decide the sample size, assign a number to every member of the sample.
Step four: Define the interval of this sample. This will be the standard distance between the elements.
For example, the sample interval should be 10, which is the result of the division of 5000 (N= size of the population) and 500 (n=size of the sample).
| Systematic Sampling Formula for interval (i) = N/n = 5000/500 = 10 |
Step five: Select the members who fit the criteria which in this case will be 1 in 10 individuals.
Step six: Randomly choose the starting member (r) of the sample and add the interval to the random number to keep adding members in the sample. r, r+i, r+2i, etc. will be the elements of the sample.
When you are sampling, ensure you represent the population fairly. Systematic sampling is a symmetrical process where the researcher chooses the samples after a specifically defined interval. Sampling like this leaves the researcher no room for bias regarding choosing the sample. To understand how it exactly works, take the example of the gym class where the instructor asks the students to line up and asks every third person to step out of the line. Here, the instructor has no influence over choosing the samples and can accurately represent the class.
For instance, if a local NGO is seeking to form a systematic sample of 500 volunteers from a population of 5000, they can select every 10th person in the population to build a sample systematically.
Here are the types of systematic sampling:
Let’s take a closer look at these sampling techniques.
Systematic random sampling is a method to select samples at a particular preset interval. As a researcher, select a random starting point between 1 and the sampling interval. Below are the example steps to set up a systematic random sample:
Linear systematic sampling is a method where samples aren’t repeated at the end and ‘n’ units are selected to be a part of a sample having ‘N’ population units. Rather than selecting these ‘n’ units of a sample randomly, a researcher can apply a skip logic to select these. It follows a linear path and then stops at the end of a particular population.
This sampling or skip interval (k) = N (total population units)/n (sample size)
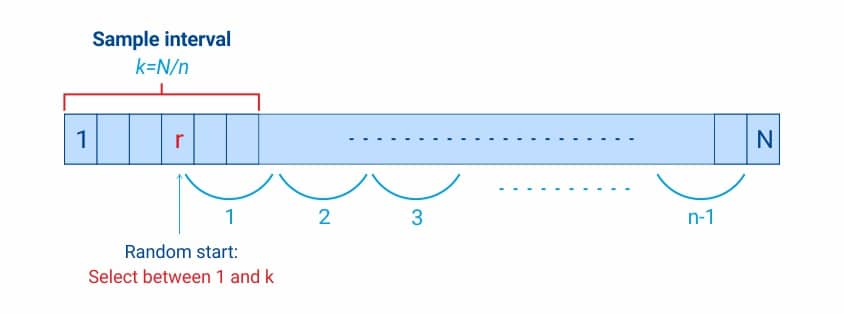
How is a Linear systematic sample selected?
In circular systematic sampling, a sample starts again from the same point once again after ending; thus, the name. For example, if N = 7 and n = 2, k=3.5. There are two probable ways to form sample:
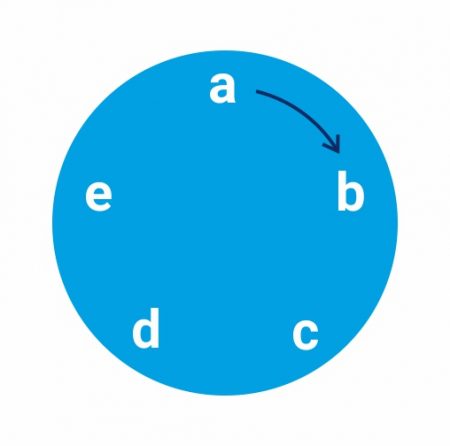
How is a circular systematic sample selected?
Here is the difference between linear and circular.
Here are the advantages:
Other probability sampling techniques like cluster sampling and stratified random sampling can be very unorganized and challenging due to which researchers and statisticians have turned to methods like systematic sampling or simple random sampling for better sampling results. It consumes the least time as it requires a selection bias of sample size and identification of the starting point for this sample, which needs to be continued at regular intervals to form a sample.
Let’s take an example where you want to form a sample of 500 individuals out of a population of 5000; you’d have to number every person in the population.
Once the numbering is done, the researcher can select a number randomly, for instance, 5. The 5th individual will be the first to be a part of the systematic sample. After that, the 10th member will be added into the sample, so on and so forth (15th, 25th, 35, 45th, and members till 4995).
Here are 4 other situations of when to use Systematic Sampling:
QuestionPro Audience has a global sample of 22 million+ survey respondents who are double-opted and mobile-ready to participate in all levels of market research and brand research. Need niche panelists like gamers, building contractors, directly get in touch with our niche panelists.